1.1. 복소수
양자 컴퓨팅을 이해하려면 복소수의 성질을 어느 정도 알아야 한다. 복소수는 실수와 허수라는 두 가지 기수(fundamental numbers)로 이뤄지고, 이차 방정식의 해가 될 수 있다. 복소수 c 는 다음과 같다.
c = a + bi
위 식에서 a 와 b 는 실수고, i 는 √(-1) 이다. 숫자 a 는 c 의 실수부, 숫자 b는 c 의 허수부이며, 다음과 같이 표현할 수 있다.
a = c 의 실수부 = Re(a + bi)
b = c 의 허수부 = Im(a + bi) [1]
실수와 허수는 복소수의 부분집합이며, Re(a + bi) = 0 이면 c 는 순허수, Im(a + bi) = 0 이면 c 는 실수이다. 0 의 경우, 0 = 0 + 0i 이므로 실수이자, 순허수이다.
그림 1.1 복소평면
복소 평면(complex plane)은 실수부 a 를 x 좌표로, 허수부 b 를 y 좌표로 하는 점으로 표시한다. 수평축은 실수축(real axis), 수직축은 허수축(imaginary axis)이라고 한다.
복소수의 크기(magnitude) 및 길이(length)는 피타고라스 정리를 이용하여, 실수부와 허수부를 제곱해 더한 값의 제곱근으로 구할 수 있다.
|c| = √(a²+ b²)
복소수 i²= -1 이라는 점만 염두하면, 연산 규칙은 다음과 같다.
덧셈 : (a + bi) + (b + di) = (a + c) + (b + d)i
곱셈 : (a + bi) x (b + di) = ac + adi + bci - bd = (ac + bd) + (ad + bc)i
나눗셈[2] : (a + bi) / (c + di) = ((ac + bd) + (bc - ad)i) / (c2 + d2)
1.2. 켤레복소수
복소수 c 의 켤레복소수는 허수부의 부호를 치환하며, c* 로 표기한다.
c* = a - bi
복소 평면에서는 실수축을 기준으로 반사한 복소수이다.
그림 1.2 켤레복소수
대수식의 결레복소수는 다음 세 가지 관계를 이용한다.
1. 합의 켤레는 켤레의 합과 같다. 즉, (a + b)* = a* + b*
2. 곱의 켤레는 켤레의 곱과 같다. 즉, (ab)* = a*b*
3. 켤레의 켤레는 원래의 복소수다. 즉, (a*)* = a
복소수 c = a + bi 의 법(modulus) 또는 절댓값(absolute value)는 |c| 로 표기하며, 복소 평면의 원점에서 점 c 까지의 거리이다. 자연스럽게, |c| 는 c 에 대응하는 벡터의 길이가 된다.
c 의 절댓값 제곱(square modulus)은 |c|² 로 표기하며, c 와 켤레복소수 c* 의 곱이다. cc* = |c|² 은 실수이며, 양의 값임을 아래와 같이 보일 수 있다.
cc* = (a + bi)(a - bi) = a² + b² = (√(a² + b²))(√(a² + b²)) = |c|²
복소수의 절댓값은 크기라고도 하며, 다음과 같이 표현한다.
|c| = √(cc*) = √(a² + b²)
c 의 절댓값 제곱과 c² 은 같지 않다는 점에 유의한다. c = a + bi 이므로, c² 은 다음과 같다.
c² = (a² - b²) + (2ab)i
절대값 제곱은 항상 양의 실수인 반면, 제곱은 일반적으로 복소수가 된다.
1.3. 벡터 공간
벡터 공간 V 는 벡터인 원소, 그리고 스칼라인 원소의 집합인 체(field) F 와 두 가지 연산, 벡터 덧셈과 스칼라 곱으로 이뤄진다. 체는 a 와 b 가 F 에 속하면 a + b, a - b, ab, a/b 또한 F 에 속하는 성질을 지닌 스칼라의 집합이다(a/b 에서 b ≠ 0 을 가정).
- 벡터 덧셈 : V 의 어떤 두 벡터 u 와 v 를 취해 u + v 라는 제 3의 벡터를 산출하며, 다음의 조건을 따른다.
- 닫힘성 : u + v 는 V 에 속하는 벡터다.
- 교환성 : u + v = v + u
- 결합성 : (u + v) + w = u + (v + w)
- 항등원 : V 의 모든 u 에 대해 (u + 0) = u 인 영 벡터 0 이 있다.
- 역원 : V 의 모든 u 에 대해 -u 라고 표기하며, u + (-u) = 0 인 벡터가 있다.
- 스칼라 곱셈 : F 의 스칼라 c 와 V 의 벡터 v를 취해 V 에 속하는 새로운 벡터 cv 를 산출하며, 다음의 조건을 만족한다.
- 닫힘성 : cv는 V 에 속한다.
- 분배성1 : c(u + v) = cu + cv // 스칼라 값이 분배
- 분배성2 : (c + d)u = cu + du // 벡터가 분배됨
- 결합성 : c(du) = (cd)u
- 항등원 : 1(u) = u
예를 들어, 복소 벡터 공간 Cⁿ 의 두 복소 벡터 X와 Y 가 있다고 하자.
X = (x₁, x₂, ..., xn), Y = (y₁, y₂, ..., yn)
덧셈 연산은 아래와 같이 성분 별로 더한다.
X + Y = (x₁ + y₁, x₂ + y₂, ..., xn + yn)
곱셈 연산은 각 성분 X(또는 Y)에 복소수 c 를 곱해준다.
c(X) = (cx₁, cx₂, ..., cxn)
1.4. 기저 집합
고전 물리학이 3차원 공간의 위치를 직교하는 세 축 x, y, z 좌표로 결정하듯이, 유사한 개념으로 양자역학에는 상태 벡터(state vector)로 표현하며, 이때 기저 집합(basis set)을 이용한다. 어떤 벡터 공간의 기저 집합은 해당 벡터 공간의 모든 벡터를 유일한 일차 결합(Linear combination)으로 표현할 수 있는 벡터들의 부분 집합이다.
기저 집합에 속한 벡터 중 어느 벡터도 기저 집합의 다른 벡터의 일차 결합으로 표현하지 못한다. 일반적으로 n 차원 벡터 공간은 다른 n 개의 벡터로 이뤄진다. 각 기저 집합의 모든 벡터의 크기가 1이면서, 각 벡터가 다른 벡터와 수직인 기저를 정규 직교 기저(orthonormal basis)라고 한다. 예를 들어, 다음 단위 벡터 i, j, k 는 일반적인 3차원 벡터 공간에 정규 직교 기저를 이루며, 표준 단위 벡터이다.
어떤 벡터든지 표준 단위 벡터의 일차 결합으로 나타낼 수 있다.
내적(inner product) 함수는 두 벡터를 이루는 수로 나타내며, 데카르트 3차원 공간에서 두 벡터 u 와 v 의 내적은 다음과 같이 정의된다.
uㆍv = uxyx + uyvy + uzvz
길이는 벡터의 노름(norm) 이라고도 하며, 벡터 u 의 길이는 √(uㆍu) 이다.
양자 컴퓨팅에서 벡터는 복소 벡터 공간(complex vector space)에 속하며, N차원 복소 벡터 공간의 벡터 v는 다음과 같이 나타낸다.
v ∈ CN
N차원 벡터 공간은 N개의 기저 벡터와 N개의 성분을 가지며, 다음과 같이 열 표현(column representation)한다.
복소 공간에서 두 벡터 u 와 v 의 내적은 <u v> 로 표기하며, u 와 v 를 입력으로 받아 복소수를 결과로 산출하는 함수이다. 내적 <u v> 는 다음과 같이 계산한다.
예를 들어 양자 상태 w1 과 w2 가 다음과 같이 복소 벡터 공간의 두 열벡터로 표현되면,
두 상태의 내적은 w₁ 의 켤레복소수를 취한 후 두 벡터의 대응 성분을 곱하고, 마지막으로 곱한 결과를 합친다.
1.5. 디랙 표기법
양자역학에서 양자 상태는 디랙 표기법(Dirac notation)으로 표현한다. 두 벡터 u 와 v 의 내적은 <u|v>로 표기하며, 왼쪽의 <u| 부분을 브라(bra), 오른쪽의 |v> 부분을 켓(ket) 이라고 부른다. 내적을 <>(braket) 으로 표기하므로, 디랙 표기법을 브라-켓 표기법(bra-ket notation)이라고도 한다.1.5.1. 켓
복소 벡터 공간 V 에 속하는 벡터 v 를 켓으로 다음과 같이 표기한다.
|v> ε V
켓은 열벡터와 유사하다. 복소 벡터 공간이므로, 열벡터의 모든 항은 복소수다. 예를 들어, N 개의 기저 벡터 |i> 가 있고, i = 0, 1, ..., N-1 일 때 임의의 벡터 |v> 를 다음과 같이 쓸 수 있다.
여기서 ci는 임의의 복소수 집합이다. 이를 N 개의 복소 열벡터로 다음과 같이 나타낼 수 있다.
(|Ψ> + |φ>) = |ω> = (|φ> + |Ψ>)
또한 켓의 덧셈은 결합 가능하며, 덧셈 연산에 닫혀있다.
(|Ψ> + |φ>) + |ω> = |Ψ> + (|φ> + |ω>)
켓의 성질을 정리하면 다음과 같다.
- (c₁ + c₂)|u> = c₁|u> + c₂|u>
- c₁(c₂|u>) = (c₁c₂)|u>
- c(|u> + |v>) = c|u> + c|v>
- 1|u> = |u>
- |u> + |0> = |u>
양자 컴퓨팅에서는 오직 복소 벡터 공간만 다루므로, 스칼라 c 또한 복소수이다. 복소수 c 와 켓 |u> 의 곱은 줄 중 어느 순서로 써도 된다.
c|u> = |u>c
벡터 공간에는 영 벡터(null vector, zero vector)라는 특수한 벡터가 있다. 영 벡터는 0이라고 쓰며, |0> 이라고 쓰지 않는다. 따라서 다음과 같다.
|u> + 0 = |u>
0|u> = 0
1.5.2. 브라
선형대수에서는 열벡터와 행벡터를 모두 사용하지만, 디랙 표기법에서는 브라(bra)라는 기호를 서서 행벡터를 표현한다. 켓 |0> 과 |1>에 대응하는 브라는 다음과 같다.
<0| = (1 0)
<1| = (0 1)
복소 벡터 공간 V 에는 모든 켓에 대해 유일한 브라가 있다. 어떤 켓에 대응되는 브라는 켓에 켤레 전치( conjugate transpose)를 취해 얻으며, 그 반대도 마찬가지다. 브라 <u|가 벡터 v 에 작용하면 벡터를 복소수 c 로 바꾼다. 이를 다음과 같이 쓸 수 있다.
<u|:v → c
예를 들어, v 는 켓 표기법으로 다음과 같이 쓴다.
<u|(|v>) = c
또는 간단히 다음과 같이 쓴다.
<u | v> = c
위의 식은 <u| 를 임의의 켓 벡터 |v> 와 결합해 복소수 c 를 얻을 수 있음을 나타낸다. <u| 라는 양(quantity)은 V 의 모든 벡터에 복소수를 할당하는 함수로 간주할 수 있으며, 이러한 함수를 선형 범함수(linear functional)라고 한다. 반대로, 브라 벡터를 켓 벡터에 작용해 복소수를 산출하는 연산자로 해석할 수도 있다.
켓 |1> 과 |0> 에 대응되는 브라는 각 켓의 켤레 전치다.
<1| = [0 1] <0| = [1 0]
브라는 확률 진폭(probability amplitude) 을 계산할 때 유용하다. 확률 진폭은 확률과 비슷하나 값이 복소수이며, 양자의 상태를 표현하는 데 사용된다. 양자 수준에서는 관측 전까지 여러 상태가 확률적으로 중첩되며, 이러한 특성에 따라 큐비트는 값이 0 이면서 동시에 1 일 수 있다. 두 개의 확률 진폭을 사용해 하나의 큐비트를 α|0> + β|1> 로 나타내며, 이 큐비트의 값이 0일 확률은 |α|², 1일 확률은 |β|² 이다.
큐비트의 상태가 |1> 에 있을 확률은 일반적인 큐비트 상태를 브라 <1| 과 결합하여 다음과 같이 결정할 수 있다.
<1|ψ> 라는 양은 |1> 상태에 있을 확률 진폭, <0|ψ> 상태 |0> 에 있을 확률 진폭으로 해석 가능하다. <0|1> 과 <1|0> 은 모두 0과 같으며, 이를 직교 상태라고 한다. 진폭 <0|0> 과 <1|1> 은 모두 1과 같다. 어떤 양자 상태 |ψ> 에 대해 진폭은 <ψ|ψ> = 1 이다.
|ψ> = α|0> + β|1> 이므로, 이와 동반되는 쌍대(dual) 또는 브라는 다음과 같다.
<ψ| = α*<0| + β*<1|
따라서 진폭 <ψ|ψ> 는 다음과 같이 계산할 수 있다.
두 브라의 합은 다음과 같이 유도할 수 있다.
(<c₁| + <c₂|)|v> = <c₁|(|v>) + <c₂|(v>)
예를 들어, 두 개의 켓이 다음과 같을 때,
브라는 켓의 켤레 전치이므로, 두 켓에 대응되는 브라는 아래와 같다.
<u| = (p*, q*) <v| = (i*, j*)
위 두 브라의 합은 다음과 같다.
<u + <v| = (p* + i*, q* + j*)
이는 두 켓의 합의 켤레 전치와 같다.
브라와 켓은 다음의 규칙을 따른다. 아래에서 a 는 임의의 상수다.
- <v | au> = a<v|u>
- <av | u> = a* <v | u>
- <v | u>* = <u | v>
- <u| + <v| = <u + v |
브라와 켓이 연산자로 어떻게 스였는 지에 따라 식에 나오는 브라와 켓의 순서가 달라진다. 예를 들어, <v | w> ≠ <w | v> 다.
스칼라, 즉 복소수는 식에서 이동 가능하다. 예를 들어,
|v><v | w><w| = <v | w>|v><w|
이는 <v | w>가 복소수이기 때문이다.
1.6. 내적
복소 공간의 두 벡터 u 와 v 의 내적은 <uv> 로 표기하며, 복소수를 결과로 산출한다. 내적은 다음의 성질을 만족시켜야 한다.
- 선형성(linearity) : <a | (w | b> + v | c>) = w <a | b> + v <a | c>
- 대칭성(symmetry) : <u | v> = <v | u>*
- 양부호성(positivity) : |u> ≠ 0 인 경우, <u | u> ≥ 0
내적을 갖는 벡터 공간 V 를 내적 공간(inner product space)라고 한다. 양자역학의 힐베르트 공간(Hilbert space)의 단위 벡터는 물리계와 관련된다. 힐베르트 공간은 내적을 갖는 복소 벡터 공간이다.
복소 벡터 공간의 벡터 |u> 와 |v> 의 내적을 디랙표기법으로 다음과 같이 나타낸다. 아래 식의 c 는 복소수이다.
<u | v> = c
벡터 |u> 가 다음을 만족하면 정규화된(normalized) 벡터이다.
(|u>, |u>) = 1
두 벡터 |u>, |v> 가 다음을 만족하면 두 벡터는 직교(orthogonal)한다.
(|u>, |v>) = 0
1.7. 일차 종속 벡터와 일차 독립 벡터
벡터 집합의 어던 원소를 다른 원소에서 유도하지 못하는 경우, 이 벡터 집합은 일차 독립(linearly independent)이다. 식으로 나타내면 벡터 v0, v1, v2, ... , vn-1 로 이루어진 집합이 임의의 복소 계수 c0, c1, c2, ..., cn-1 에 대해 다음을 만족하면 일차 독립이다.
c0v0 + c1v1 + c2v2 + ... + cn-1vn-1 = 0
그러면 다음과 같다.
c0 = c1 = ... = cn-1 = 0
반대로, 복소 계수 c0, c1, c2, ..., cn-1 중 일부가 0 이 아니면 벡터 v0, v1, v2, ... , vn-1 은 일차 종속(linearly dependent) 이다.
c0v0 + c1v1 + c2v2 + ... + cn-1vn-1 ≠ 0
1.8. 쌍대 벡터 공간
앞서 1.4절에서 기저 집합의 개념을 다루었다. 식으로 나타내면 벡터 집합 {v0, v1, ... , vn} 이 어떤 벡터 공간에 대해 다음 기준을 만족하는 경우 이 벡터 집합을 그 벡터 공간의 기저(basis)라고 한다.
- 벡터 집합 {|v0>, |v1>, ..., |vn>} 이 해당 벡터 공간을 생성(span)한다. 즉, 벡터 공간의 모든 상태를 이 집합에 속하는 상태의 일차 결합으로 표현할 수 있다. 다시 말해, 임의의 벡터 공간의 상태 ψ를 다음과 같이 나타낼 수 있다.
- 벡터 집합 { |v0>, |v1>, |v2>, ... , |vn> } 이 일차 독립이다.
- 벡터 집합이 완전(complete)하다. 완비성(completeness)은 양자계의 모든 가능한 물리 상태를 나타낼 때 더 이상 추가적인 기저가 필요하지 않음을 의미한다. 벡터{v0, v1, ..., vn}을 해당 벡터 공간의 기저 상태(basis state)라고 부른다.
복소 벡터 공간에서 임의의 벡터 |x> 를 기저 벡터 일차 결합으로 유일하게 표현할 수 있다.
위 식에서 복소수 ci는 기저 벡터 {v0, v1, ... , vn}에 대한 |x> 의 성분이라고 한다.
V 의 벡터 집합 {e0, ..., en}이 다음을 만족하면 정규 직교(orthonormal)이다.
<ei | ej > = δij
위 식에서 δij 는 크로네커 델타(Kronecker delta)라고 하며, i = j 인 경우에는 1, i ≠ j 인 경우에는 0 이다.
정규 직교 집합이 폐포 관계(closure relation)를 만족하면 V 의 기저이다.
내적을 디랙 표기법으로 나타낼 때 오른쪽 백터 y 를 켓 표기법으로 작성했다. 왼쪽의 <x| 라는 양(quantity)은 어떤 켓 |y> 를 내적해 복소수로 사상하는 선형 범함수(linear functional)이다.
모든 선형 범함수 집합(<x|, ... )은 V 의 쌍대 공간(dual space)인 복소 벡터 공간 V* 를 형성한다. 즉, 복소 벡터 공간 V는 모든 브라의 집합을 포함하는 쌍대 벡터 공간(dual vector space) V* 를 갖는다. 예를 들어 V 의 켓 벡터의 집합 (|v₁>, |v₂>, ... , |vn) 에 대해 쌍대 공간 V* 는 (<v₁|, <v₂|, ... , <vn|)으로 이루어진다. V*의 어떤 두 원소의 합도 V*에 속하며, V*의 원소화 복소 스칼라의 곱 또한 V* 의 원소이다.
V 와 V*가 동일한 공간이 아니지만, V 의 각 켓 벡터 |y> 에 대해 대응되는 V* 의 브라 벡터 <y| 가 존재한다는 점에 유의한다.
|y> = (<y|)*<y| = (|y>)*
쌍대 공간 V*에서 두 브라의 합도 V*의 브라이며, 복소수와 브라의 곱도 V*의 브라가 된다.
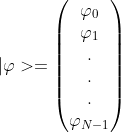
벡터 공간 V와 그 쌍대 공간 V*의 차원은 같다. V와 V*의 벡터들은 각각 열 행렬(column matrix)과 행 행렬(row matrix)로 표현된다. |φ>가 다음의 n차원 열벡터를 나타낸다고 가정하자.
<φ| 로 표기하는 쌍대 벡터는 다음과 같이 정의된다.
<φ| = (φ0*, φ1*, ... , φN-1*)
켓이 열벡터로 표현되면 브라는 행벡터로 볼 수 있다. 브라를 왼쪽에 두고 켓을 오른쪽에 두어 내적을 표기하면 행렬 곱의 규칙에 따라 행벡터와 열벡터를 곱해 숫자를 결과로 얻는다.
1.9. 계산 기저
모든 벡터 공간에는 무한한 수의 정규 직교 기저가 있다. 실제 사용하는 기저 집합은 특별한 이유가 있는 기저 집합보다는 사용하기 쉬운 기저 집합이 선택되며, 이러한 기저를 계산 기저(computational basis)라고 한다. 기저 집합이 유일할 필요는 없지만, 집합에 포함된 기저 벡터의 개수는 불변이다. 예를 들어 복소 벡터공간 Cⁿ 의 기저가 n 개의 일차 독립 벡터로 이뤄졌다고 가정해보자. 그러면 Cⁿ 의 임의의 벡터 |x> 를 n 개 벡터의 일차 결합으로 유일하게 표현할 수 있다.
여기에서 ci 는 복소수이며, |vi>는 i 번째 기저 벡터다. 기저 벡터는 특정 기저 벡터에 해당하는 위치만 1인 열벡터다.
양자 정보 처리에서는 큐비트에 대한 상태 |0> 과 |1> 을 표준 계산 기저로 사용한다. 그러나 다른 기저도 쓰인다. 예를 들어 다음의 벡터를 정규 직교 기저로 사용할 수 있다.
이 벡터 각각을 표준 계산 기저를 이용해 정의할 수 있으며, 또 다른 기저 + / - 를 형성한다.
+ / - 기저는 완비 정규 직교 기저(complete orthonormal basis)이다. 따라서 어떤 큐비트 상태든지 기저 상태 + / - 를 사용해 표현할 수 있으며, 이 기저를 하다마드 기저(Hadamard basis) 또는 대각 기저(diagonal basis)라고도 한다.
1.10. 외적
u 와 v 사이의 외적(outer product)은 다음과 같이 쓴다. 순서가 바뀐다..?
|v><u|
u 와 v 를 다음과 같이 정의하면,
u 와 v 의 외적은 다음과 같으며, 결과는 복소수가 아니라 행렬이다.
외적 |v><u| 를 연산자 A로 해석할 수 있다. A = |v><u| 이면 상태 φ 에 대한 A 의 동작은 다음과 같다.
Aφ = (|v><u|)φ = |v>(<u|φ>) = |v><u|φ>
[1] 허수는 영어로 Imaginary number 이다. 실수는 Real number.
[2] 허수부의 부호를 반대로 하는 켤레 복소수 c - di 를 분자와 분모에 곱한다. 즉, ((a + bi) / (c + di)) x ((c - di) / (c - di)) 를 정리한다. 이 과정을 '분모의 실수화'라고 한다. 출처는 아래 블로그.

















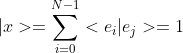







댓글 없음:
댓글 쓰기